essai_clinique_mh <- function(nchain, data, init, prop_sd){
## A commenter
acc_rate <- 0
log_dose <- data$log_doses
ndeath <- data$ndeaths
nanimals <- data$nanimals
chain <- matrix(NA, nchain + 1, 2)
colnames(chain) <- c("beta0", "beta1")
chain[1,] <- init
## proba de mourrir
death_prob <- exp(chain[1,1] + chain[1,2] * log_dose) /
(1 + exp(chain[1,1] + chain[1,2] * log_dose))
for (iter in 1:nchain){
## générons un candidat par une perturbation gaussienne de l'état actuel
prop <- rnorm(2, chain[iter,], prop_sd)
## Calculons la proba de décès associée
## à ces paramètres candidats
death_prob_prop <- exp(prop[1] + prop[2] * log_dose) /
(1 + exp(prop[1] + prop[2] * log_dose))
## Calcul de la proba d'acceptation
top <- sum(dbinom(ndeath, nanimals, death_prob_prop, log = TRUE))
bottom <- sum(dbinom(ndeath, nanimals, death_prob, log = TRUE))
acc_prob <- exp(top - bottom)##sans le min(1, ...) qui ne sert à rien algorithmiquement
## Phase d'acceptation rejet
if (runif(1) < acc_prob){
chain[iter+1,] <- prop
death_prob <- death_prob_prop
acc_rate <- acc_rate + 1
} else{
chain[iter+1,] <- chain[iter,]
}
}
ans <- list(chain = chain, acc_rate = acc_rate / nchain)
}Essai clinique
On souhaite estimer le \(LD_{50}\), i.e., le dosage pour lequel on a 1 chance sur 2 de mourrir. Pour cela, on dispose des données :
| Dose \(x_i\) (log g / mL) | Nombre d’animaux testés \(n_i\) | Nombre de décès \(y_i\) |
|---|---|---|
| -0.86 | 5 | 0 |
| -0.30 | 5 | 1 |
| -0.05 | 5 | 3 |
| 0.73 | 5 | 5 |
Clairement, le nombre de décès corresponds au nombre de “succès” parmi un nombre donné de tentatives. Cela justifie l’utilisation d’un modèle Binomial. Plus précisément, on pose : \[Y_i \mid X_i \stackrel{ind}{\sim} \mbox{Bin}(n_i, \theta_i),\] où la probabilité de mourrir \(\theta_i\) dépend naturellement du (log)-dosage et est donnée par \[\mbox{logit}(\theta_i) = \beta_0 + \beta_1 x_i.\]
Inférence Bayésienne sur un essai clinique
Nous allons travailler dans un cadre Bayésien et donc mettre une loi a priori (non informative de type Laplace) sur les paramètres du modèle \(\beta_0\) et \(\beta_1\). La loi a posteriori est donnée par \[\pi(\beta_0, \beta_1 \mid y) \propto \prod_{i=1}^4 \left[ \theta_i^{y_i} (1 - \theta_i)^{n_i - y_i} \right]\]
Algorithme de Metropolis-Hastings
Analyse
Testons donc notre code sur le jeu de données.
data <- data.frame(log_doses = c(-0.86, -0.3, -0.05, 0.73),
nanimals = rep(5, 4),
ndeaths = c(0, 1, 3, 5))
nchain <- 10^4
init <- c(0, 0)##<-- proba de mourir = 1/2 quelque soit le dosage
prop_sd <- c(1, 1)### <-- au pif pour la 1ère fois puis on affine
tmp <- essai_clinique_mh(nchain, data, init, prop_sd)Analysons la chaine simulée.
chain <- tmp$chain
acc_rate <- tmp$acc_rate
library(coda)##juste pour le graphe (y a d'autres trucs)
plot(mcmc(chain))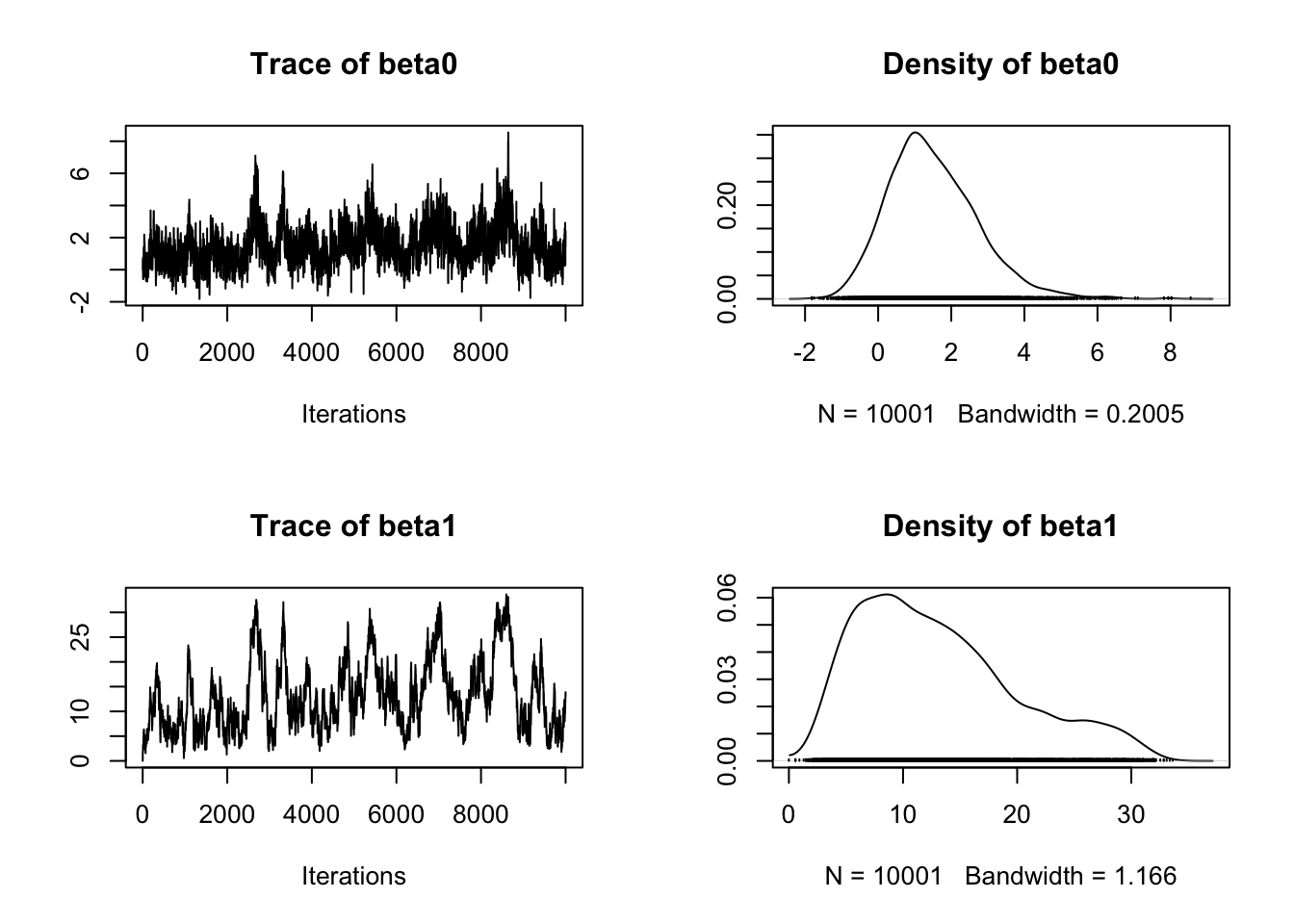
Sur ce premier essai de chaine simulée, on voit que (notamment pour \(\beta_1\)) la chaine ne mélange pas très bien avec des “petits déplacement”. C’est confirmé par le taux d’acception proche de 65%. Augmentons l’écart type de proposition.
prop_sd <- c(2, 3)
tmp <- essai_clinique_mh(nchain, data, init, prop_sd)
chain <- tmp$chain
acc_rate <- tmp$acc_rate
plot(mcmc(chain))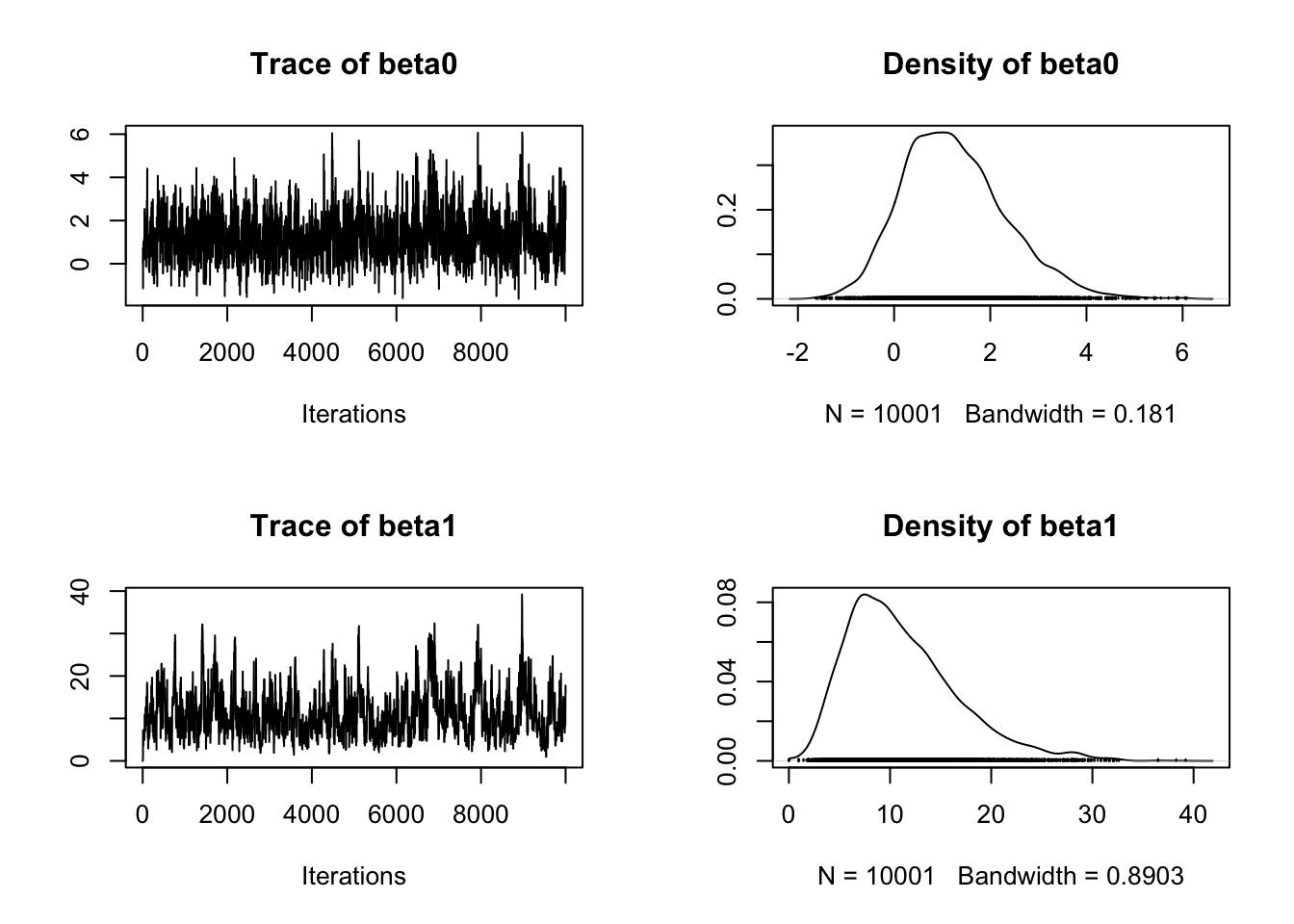
Le code est ultra rapide, je peux donc me permettre de simuler une chaine longue et l’élaguer. Faisons cela pour voir l’effet de l’élagage.
prop_sd <- c(2, 3)
nchain <- 10^5
tmp <- essai_clinique_mh(nchain, data, init, prop_sd)
chain <- tmp$chain
acc_rate <- tmp$acc_rate
par(mfrow = c(2, 2))
for (j in 1:2){
acf(chain[,j])
acf(chain[seq(1, nchain, by = 5),j])
}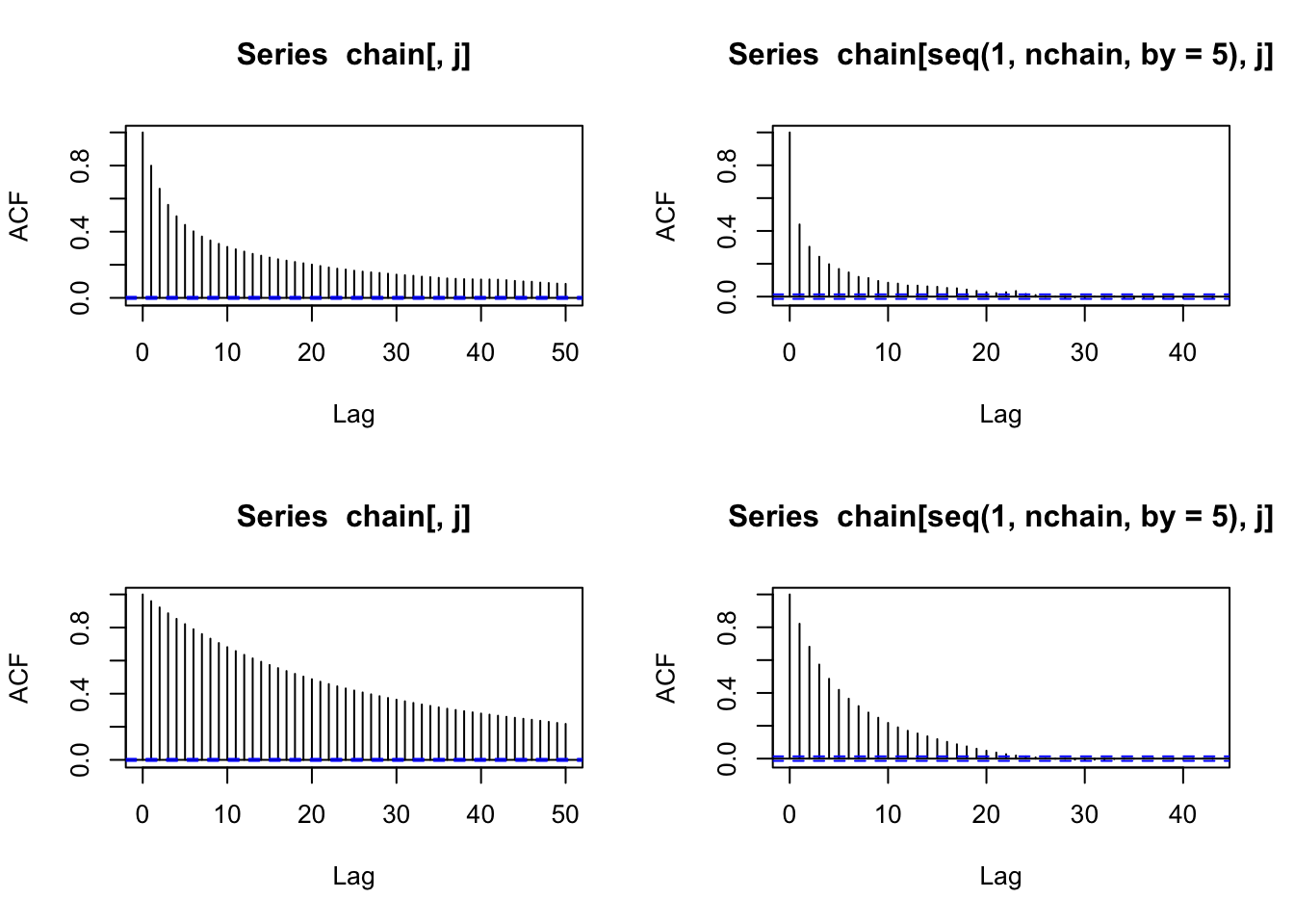
On pourrait mieux faire mais on s’arrête. (Idéalement augmenter l’écart-type de proposition pour \(\beta_1\).)
Attention : ici pas besoin de supprimer la période de chauffe mais ça ne sera pas toujours le cas !
final_chain <- chain[seq(100, nchain, by = 5),]Vérifions la qualité d’ajustement de notre modèle. Pour cela on compare le nombre de décès observés par celui attendu sous notre modèle.
## Estimation par moyenne a posteriori
beta_hat <- colMeans(final_chain)
## Nombre attendu de décès
proba_death_hat <- exp(beta_hat[1] + beta_hat[2] * data$log_doses) / (1 + exp(beta_hat[1] + beta_hat[2] * data$log_doses))
print(rbind(obs = data$ndeaths, exp = data$nanimals * proba_death_hat)) [,1] [,2] [,3] [,4]
obs 0.0000000000 1.0000000 3.000000 5.000000
exp 0.0007894261 0.5035365 3.386082 4.999745Le modèle semble plutôt bon. Je suis content. (on aurait pu valider cela par un test d’adéquation du \(\chi^2\).)
Estimons el famoso \(LD_{50}\). Faisons un peu les maths. Appelons \(x_*\) ce dosage. \[\frac{\exp(\beta_0 + \beta_1 x_*)}{1 + \exp(\beta_0 + \beta_1 x_*)} = \frac{1}{2} \Longleftrightarrow \beta_0 + \beta_1 x_* = 0 \Longleftrightarrow x_* = -\frac{\beta_0}{\beta_1}.\] Ici, puisque l’on est dans un cadre Bayésien, on ne va pas utiliser un estimateur de type plugin, i.e., en remplaçant \(\beta_0\) et \(\beta_1\) par leurs estimations respectives, mais en utilisant la chaine toute entière. Cela permet d’avoir la loi a posteriori du \(LD_{50}\).
LD50 <- exp(-final_chain[,"beta0"] / final_chain[,"beta1"])
## on passe à l'exponentielle pour ne plus avoir le log-dosage
par(mfrow = c(1,2))
plot(LD50)
plot(density(LD50))
print(c(mean(LD50), quantile(LD50, prob = c(0.025, 0.975)))) 2.5% 97.5%
0.9028891 0.7594113 1.1099182 Le dosage \(LD_{50}\) est donc estimé (via la moyenne a posteriori) à 0.9 avec un intervalle de crédibilité à 95% de [ 0.76, 1.11].