The Self-Driving Taxi challenge

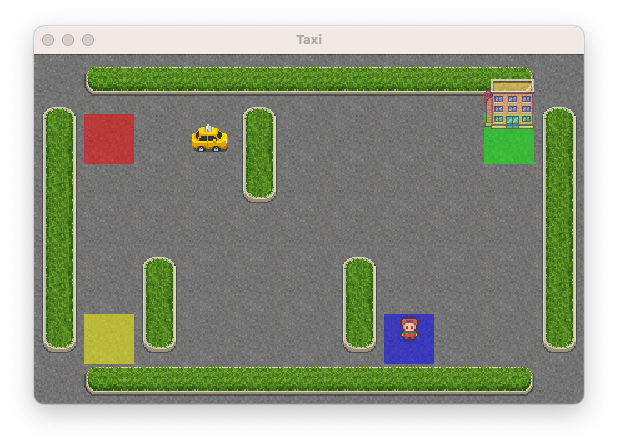
Here are the rules of the game. The taxi will pick up a passenger at one location and drop them at another place. But in doing so our self-driving taxi should:

- drop off the passenger at the right location
- minimizing the travel time
- take care of traffic rules

Since we are going to use a Markov decision process we need to define :

- the state space
- the action space
- the reward function

Reward function

- successful dropoff gives a (large) positive reward
- penalty if dropoff to the wrong location
- small penalty for each move

State space

The taxi will drive in a 5 x 5 pixel grid where some wall exists. We have 4 specific locations on that grid where we can pick up and dropoff passengers. The taxi can be occupied or not.

Action space

The possible actions are:

- going south, north, east or west
- pickup or dropoff passenger

OpenAI Gym

This environment is very famous for testing reinforcement learning algorithm. It provides many many situations such as our previous self driving taxi problem. We first need to install it (you should be able to do it by yourself) and then import our Taxi problem by invoking:

import gymnasium as gym
env = gym.make("Taxi-v3", render_mode = "human").env

Question 1:

Run the following code and make sure you understand what you see

print(env.action_space)
print(env.observation_space)
env.reset()
env.render()

state = env.encode(2, 2, 0, 0)## (taxi row, taxi colum, passenger status, destination index)
env.s = state
env.render()

env.step(2)##changes 2 to other values
print(state)
env.render()
env.close()

Discrete(6)
Discrete(500)
240

Question 2:

In the above output:

- why do we have Discrete(6)?
- why do we have Discrete(500)?

## Answer goes here

Question 3:

Play with a bit with this game using the method step to pickup a passenger and drop him off at a wrong / right place.

## Have fun here!

Question 4:

Could you tell what is the "reward" if:

- we try to dropoff a passenger at a wrong location?
- we move from one cell to a neighbouring one (or facing a wall)?
- we dropoff a passenger to the right location?

## Answer goes here

Question 5:

Write a small code which performs a completely random policy to drive your passengers and ouput the number of travels done before successfully dropoff a passenger as well as the number of penalties, i.e., temptative to dropoff at a wrong location. Watch out: You may want to put a maximum number of iteration to prevent the game taking too much time.

## %load solutions/question_5.py

Question 6:

Implement a $q$-learning strategy with $\alpha = 0.05$ and $\gamma = 1$. Why did we set $\gamma = 1$? While learning the optimal policy, you may notice that the learning speed increase over episode. Why is it so? Note that for pedagogical purposes, I did set a learning rate too low.

Remark: You may want to consider a very large number of simulated episode, e.g., $N = 10^4$.

# %load solutions/question_6.py

Question 7:

Write a function performance that evaluates the performance of a given policy by running a couple, say 100, of episodes and showing the average number of penalties, average number of moves.

# %load solutions/question_7.py

Question 8:

Using the just learnt $q$-table, estimate the performance of the associated policy and compare your results to the completely random policy.

# %load solutions/question_8.py

Question 9:

Implement a $q$-learning strategy where you rather opt for $\epsilon$-greedy improvement policy during the learning stage (with $\epsilon = 0.1$). Compare your results to the greedy improvement.

Remark: You may want to use a burnin period where for the say, first 1000 steps, you just explore.

# %load solutions/question_9.py

Question 10:

Implement a variant of the $\epsilon$-greedy improvement policy where now $\epsilon$ is actually a decreasing sequence $\{\epsilon_n\colon n \geq 1\}$ such that $\epsilon_t \to 0$.

# Code goes here